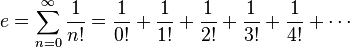Dividing decimals by decimals

When dividing decimals by decimals, such as 45.89 ÷ 0.006, we are told to move the decimal point in both the dividend and the divisor so many steps that the divisor becomes a whole number. Then, you use long division. But why?

Schoolbooks often don't tell us the "why", just the "how".

This video explores this concept.


Divide decimals - why do we move the decimal point?


It has to do with the fact that when we move the decimal point, we are multiplying both numbers by 10, 100, 1000, or some other power of ten. When the dividend and the divisor are multiplied by the same number, the quotient does not change. This principle makes sense:

0.344 ÷ 0.004 can be thought of, "How many times does four thousandths fit into 344 thousandths?"

The same number of times as what four fits into 344!

So, 0.344 ÷ 0.004 can be changed into the division problem 344 ÷ 4 without changing the answer. Both 0.344 and 0.004 got multiplied by 1000.

When we simplify fractions or write equivalent fractions, we use the same principle. Remember, fractions are like division problems.

3/7 is 3 ÷ 7.

And, 3/7 = 6/14. We can multiply the numerator and the denominator (or the dividend and the divisor) by some same number, without changing the value of the fraction (the quotient).

Or, 90/100 = 9/10. Or 0.9/0.2 = 9/2.

Exponent worksheets

There's a new addition at HomeschoolMath.net, free exponent worksheets.

You can create an unlimited supply of free printable exponents worksheets there. The worksheets concentrate on calculations with exponents, such as solving 3³ or (1/2)⁴ or (-5)⁰ or 8^-2. You can choose to include negative or zero exponent. You can choose fractions, decimals, or negative numbers as bases. You can also make worksheets that have one other operation besides exponentiation (several operations with powers).

World Math Day 2010

World Math Day 2010 is coming up on March 3rd. You might remember it from last year. It is a free event and lots of fun for the kids.

Registrations close March 2nd. Once you register, you can go practice at the website.

In it, students complete against other students from around the globe in REAL time, with simple mental math questions (such as 7 + 8 or 24 ÷ 4 or 9 × 9). It involves more than 2 million students from over 200 countries.

• Brand NEW format.
• Be part of setting a world record!
• Designed for all ages and ability levels. Simple to register and participate. All you need is Internet access.
• Great prizes
• And it’s absolutely free!!

Remember to hurry because the registration closes March 2nd, 2010.

www.worldmathday.com

Math Teachers at Play again

The most current edition is posted at MathRecreation. It's very interesting, with lots of variety, head on over!

Algebra problem: airplane's speed in still air

Photo by Caribb

Someone sent me this algebra problem:
An airplane flew for 6 hours with a tail wind of 60km/hr. The return flight against the same wind took 8 hours. Find the speed of the boat in still water.

Initially, this sounds like a trick problem, because you can't know the speed of the boat when all the information given is about an airplane!

But, let's assume they meant to ask the speed of the AIRPLANE in still air.

This problem has to do with constant speed. Constant speed ALWAYS involves TIME & DISTANCE.

And here we have two situations with two different speeds: First the airplane flies over there, with the wind helping. Then it flies back, and the wind is contrary of course.

It helps to organize our information in a table, once again. We'll need time, distance, and speed. And remember, speed = distance/time, or distance = speed * time. This time, time is known for both situations. Distance is not, but it is the same distance that way and back (call it d). Traveling there, the speed will be the sum of the airplane's speed (v) plus the wind speed (60). Traveling back, the wind is contrary so its speed is subtracted from the airplane's speed.

 |  Time  | Distance  | Speed
------------------------------------------
There |   6    |    d      | v + 60           
-----------------------------------------
Back |   8    |    d      | v − 60           

I'll copy the same table here, but instead of using d for distance, I'll calculate it using distance = speed × time.

 |  Time  | Distance  | Speed
------------------------------------------
There |   6    |  6(v+60)  | v + 60           
-----------------------------------------
Back |   8    |  8(v-60)  | v − 60      

Now, one just needs to find a way to make an equation... it will be a bit different in different word problems, but this time we get it from the fact that the distance over there is the same as the distance back:

6(v + 60) = 8(v − 60)

6v + 360 = 8v − 480

840 = 2v

v = 420

The speed of the airplane in still air is 420 km/h.

Check: For checking, we will calculate the distance it traveled. Traveling 6 hours with the speed (420 + 60) km/h or 480 km/h means the distance was 2,880 km. Traveling back took 8 hours, so the speed must have been 2,880 / 8 = 360 km/h, which is (420 − 60) km/h. So, the story "matches".

Celebrating e-day

Tomorrow 2/7 is e-day.

e or Euler's number is a number that is approximately 2.718281828, so that is why someone chose 2/7 as an e-day. But e is an irrational number, so its decimal expansion is never-ending and never-repeating.

Why is this number e so important that people have even named a day after it?

If you've studied calculus, you already know at least part of the story. But even if you haven't, I'll try to unravel at least the most basic feature of e.

Consider the exponential function e^x. It is graphed below.


It has one remarkable property: when you draw a tangent to it at any particular point, the SLOPE of that tangent is always the value of the function e^x at that point. See below two examples:

A tangent at 0.69 with slope 2

A tangent at -0.69 with slope 0.5

This feature is usually expressed this way: e^x is its own derivative, or the derivative of e^x is e^x. There exists NO other function with that property!

Here's also an interesting explanation about one fundamental property of e as it relates to growth: An intuitive guide to exponential functions. This guide is meant for BEGINNERS. It's not based on calculus. Instead, it starts by looking at a basic system that doubles after an amount of time, and refines this basic system to arrive at the idea of e.

But that's just for starters. The number e has popped up in all kinds of interesting places for mathematicians over the years. For example





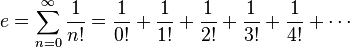
One famous equation ties in e, Pi, 1, 0, and the imaginary unit i — five important numbers in mathematics:

e^iπ + 1 = 0

See even more representations of e (infinite series, continued fractions, infinite products, and special limits). It truly is quite a number! I don't claim to understand why it is involved in all these things - like I said, it seems to "pop up" in all kinds of places. But maybe you can see a glimpse of why it is so special.

---

Curiously, in some places, e-day means something different from a day dedicated to the number e. But to celebrate the e-day in honor of the number e, whatever your language, I suggest making or baking a food that either starts with "e" or has "e" as a prominent part of its name... such as chEEsE or browniEs. It's your choice!